Teaching Math Under Common Core: Fact and Fiction, Part V

As part of a continuing discussion on the myths and truths surrounding Common Core, this piece studies the standards’ math guidelines, and addresses pertinent questions and concerns regarding the material.
Question: Is the Common Core Dumbing Math Down?
Answer: No. Most of the backlash against some of the new approaches to arithmetic are due to their novelty, not their merit.
When a sample addition problem began circulating on the internet, some parents worried that new Common Core standards were selling mathematics short. In the picture below, a student can do a subtraction problem by counting up, using easy numbers, to span the gap between the smaller number and the larger number:
The method in the bottom half of the page has been ridiculed, but math teacher Hemant Mehta thinks it makes a fair amount of sense. He explains that the rule on the top is familiar to all of us adults, but it’s not particularly intuitive to a child:
The problem with that method is that if I ask students to explain why it works, they’d have a really hard time explaining it to me. They might be able to do the computation, but they don’t get the math behind it. For some people, that’s fine. For math teachers, that’s a problem because it means a lot of students won’t be able to grasp other math concepts in the future because they never really developed “number sense.” …
If students can get a handle on thinking this way instead of just plugging numbers into a formula, the thinking goes, it’ll make other math skills much easier to understand.
Mehta’s perspective echoes the reasoning given in the Common Core downloadable math standards, which state:
There is a world of difference between a student who can summon a mnemonic device to expand a product such as (a + b)(x + y) and a student who can explain where the mnemonic comes from. The student who can explain the rule understands the mathematics, and may have a better chance to succeed at a less familiar task such as expanding (a + b + c)(x + y). Mathematical understanding and procedural skill are equally important, and both are assessable using mathematical tasks of sufficient richness.
Question: These rules might be more intuitive, but are they slower or more cumbersome than the old way?
Answer: In the short term, perhaps, but these skills exist to cultivate number sense more than to speed up calculations.
On the “Utahns Against Common Core” website, M.J. McDermott has a video that defends standard double-digit multiplication against the “cluster problems” or “partial products method” that break problems down in the same style as the addition example. “Students who learn math via [this curriculum] rarely become efficient, confident, and fluent math users,” she says on the video. It’s true that new methods may be slower, but, at the lower grade levels, teachers shouldn’t just be optimized for the speed at which students will solve problems.
When I learned my times tables, the kinds in my class used the fingers trick for remembering the nine times table. Just hold up all ten fingers, palms in, and then, counting from the left, put down the nth finger (where n is the number you’re multiplying by nine). So, for nine times four, I’d put down the ring finger on my left hand. Then, I can count the numbers on either side of the gap, and read off my hands that the product is 36.
The trick is fast, but relatively useless. (I haven’t used it since the third grade). Adults wind up memorizing multiplication because of frequent use, so, especially in an age of calculators, any computational method should end up teaching us something besides just the correct answer. The aim of these new methods is to help students get an intuitive sense for how numbers combine, not just for the answer.
Question: Are teachers and students required to use the new approaches?
Answer: No.
Common Core doesn’t mandate the old “carry the one” method, the newer “subtract by adding” method, or the Montessori “use physical objects” method. The Common Core standards just list skills and competencies that students at different grade levels are required to reach, and provides some suggested strategies for teaching them. It’s up to the school and the teacher to choose the method they think is best.
Question: Are any old techniques or subjects being discarded completely? What about Euclidean geometry?
In National Review, Michelle Malkin claimed that, under Common Core, “Traditional Euclidean geometry is replaced with an experimental approach that had not been previously pilot-tested in the U.S.” She didn’t specify what it would be replaced with (perhaps hyperbolic geometry), but the Common Core materials do not indicate that this is the case. The Common Core Introduction to Geometry reads, in part:
Although there are many types of geometry, school mathematics is devoted primarily to plane Euclidean geometry, studied both synthetically (without coordinates) and analytically (with coordinates). … During high school, students begin to formalize their geometry experiences from elementary and middle school, using more precise definitions and developing careful proofs. Later in college some students develop Euclidean and other geometries carefully from a small set of axioms.
Euclidean geometry is simply all geometry that takes place on a flat surface (e.g. shapes that are drawn on a normal sheet of paper, not the surface of a sphere). For Common Core to cut Euclidean geometry would mean, in essence, cutting geometry wholesale, and that’s not under discussion.
It’s not clear how Malkin got the impression that geometry was on the chopping block, but it’s possible she encountered the same old geometry being taught in slightly different ways, just like arithmetic, and didn’t recognize it. Ultimately, the math hasn’t changed, and it isn’t being cut.
Question: If number sense is what we’re trying to teach, will it be what the exams test?
Answer: Probably not, or at least, it won’t be the main thing they measure. Common Core determines what topics test should cover at what age, but there isn’t a set of Common Core tests that exists in the manner of AP exams. However, if the tests written for the Common Core curriculum resemble those of standardized math tests past, most of the exam will focus on what is easiest to test: whether a student came up with the right answer. The how will have to be assessed by the teacher and parents.
Stay tuned for later articles on Common Core fact and fiction, including:
– Is the Common Core initiative truly state-led?
– Could the implementation of Common Core lead to the adoption of a nationwide curriculum?
Previous posts on Common Core: Fact and Fiction—
– Fact and Fiction at CPAC Common Core Panel
– Common Core and Data Mining: Fact and Fiction, Part II
– Common Core and Informational Texts: Fact and Fiction, Part III
–Common Core and Teachers: Fact and Fiction, Part IV
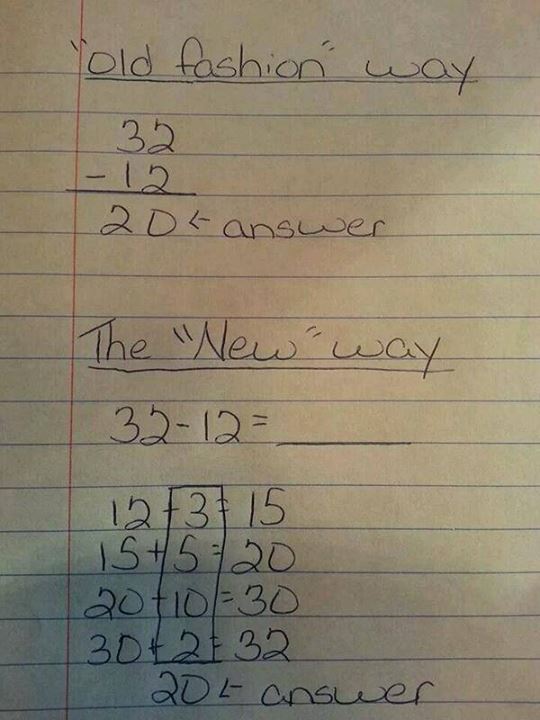
Comments