Does Pre-Crime Have a Race Problem?

The company Northpointe has a system called COMPAS that tries to predict whether a criminal will reoffend. Based on 137 criteria, each offender is given a score from 1 to 10, with higher scores meaning greater risk. Various actors in the justice system use the algorithm to make important decisions about offenders’ fates. The system is proprietary, so its precise inner workings are something of a mystery.
Race is not one of the COMPAS criteria, but in May, using data provided by Broward County, Fla., the journalism outfit ProPublica accused COMPAS of racial bias in a lengthy article accompanied by a complicated methodological appendix. (Logistic regression! Cox proportional hazard models!) The company responded with its own long, dense report, to which ProPublica has now replied.
Everyone is making this far more convoluted than it needs to be. Whatever problems there are with COMPAS, it’s relatively simple to demonstrate that it’s not racially biased in the most straightforward sense of the term. What’s more, it’s mathematically impossible to devise a rating system that will both (A) pass ProPublica’s purported test for bias and (B) provide scores that in practice mean the same thing for all racial groups. If COMPAS is biased, any system that classifies offenders this way has to be.
The key question is this: If a black person and a white person both receive the same COMPAS score, do they actually have different chances of recidivating? In a word, no. If anything, blacks with a given score often have higher reoffending rates, implying a slight bias against whites.
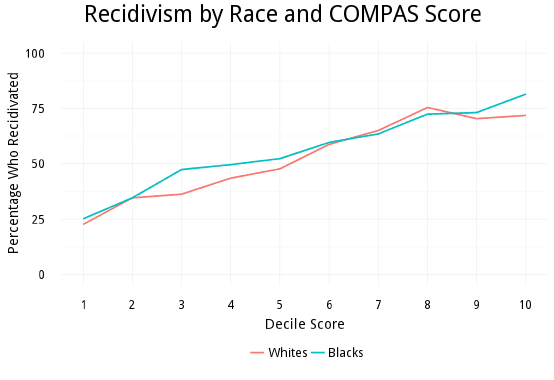
Those who read ProPublica’s report will probably be surprised by this chart, because ProPublica emphasized different numbers that, at first blush, looked quite damning. The mystery is solved with a thorough look at where those numbers come from. Here I’ll focus on the claim that 23.5 percent of whites, but 44.9 percent of blacks, were “labeled higher risk, but didn’t reoffend.” (“Low” scores are 1-4 in ProPublica’s data, while “higher” scores are 5-10.)
These are what’s called “false positive rates.” They are calculated by dividing the number of false positives—those who were classified “higher” but who didn’t actually recidivate—by the total number of people who didn’t recidivate. It answers the question: if you randomly pick someone who ultimately didn’t recidivate, what are the chances that they initially had a COMPAS score of at least 5?
The problem is that in Broward County, for whatever reason, blacks have higher recidivism rates than whites. Given that, any accurate algorithm must classify more of them as higher-risk. This necessarily means that blacks will have a higher false-positive rate. Here’s why.
Recall that the numerator is the number of false positives, i.e., people who were classified as higher risk but didn’t recidivate. Obviously, people classified as low-risk can’t be false positives, because they aren’t positives at all. So whenever you classify more people as higher-risk—even if you’re classifying them correctly—you’re increasing the number of people who will become false positives some percentage of the time. In short, the numerator is going to go up when the recidivism rate goes up.
The denominator, meanwhile, is the total number of people who didn’t recidivate. So when the recidivism rate goes up, the denominator automatically goes down, heightening the effect of the increased numerator.
For a more concrete example, say we have an amazingly precise test. There are only two categories, with exactly 75 percent of the higher category and 40 percent of the lower category reoffending. We give the test to 1,000 whites and 1,000 blacks; 500 whites but 600 blacks turn out to be higher-risk. Even in this mathematically idealized scenario we’ll have a higher numerator for blacks (150 vs. 125 false positives, or 25 percent of those labeled high-risk) and a higher denominator for whites (425 vs. 390, or the total number of people who didn’t reoffend). The false positive rates will be 38 percent for blacks and 29 percent for whites.
Ironically, the only way to avoid the problem is to make the algorithm biased in the obvious sense, so the categories mean different things depending on what race the offender belongs to. In the example above, we could randomly reassign about one-quarter of the high-risk blacks to the low-risk category to bring their false-positive rate down to that of whites. But then a low-risk designation would mean roughly a 50 percent chance of recidivism, instead of 40 percent, when the offender was black.
To be clear, there are some serious objections to systems like COMPAS. Some are uncomfortable with using algorithms to determine criminal-justice outcomes, period, even if it could reduce incarceration by identifying those who don’t pose a threat to society. Others object (quite correctly in my view) to the fact that COMPAS’s details are proprietary, making the results rather hard to dispute in court. Still others might argue against using official recidivism data, saying it comes from a biased justice system.
We should debate these issues. But let’s not demand the impossible.
Robert VerBruggen is managing editor of The American Conservative. Follow @RAVerBruggen
Comments